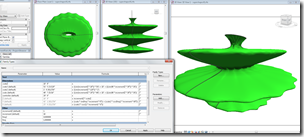
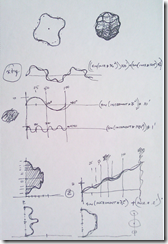
Andrew Marsh did a post recently on supershapes, these wonderfully complex parametric shapes that vary wildly depending on 8 inputs. Nathan Miller did a Grasshopper definition a couple years ago to create supershapes in Rhino. I’ve been kind of distracted by these since I started to understand the math behind them and have some experimental first stabs in Vasari/Revit. I don’t entirely understand the true mathematical definition of supershapes, but I do get the essence: if you have an ellipse and you wiggle the perimeter, then you make a bunch of these wiggly ellipses and loft a form through them, you get some whacky stuff.
Try out the families if you are feeling masochistic (c’mon, admit it, you kind of like it). They are super-unfriendly both in terms of understanding what levers to pull to get new result and regeneration times. I haven’t broken out the 8 parameters into easy manipulators, hopefully I’ll get to it. Basic idea is that the supershapesBuildz.rfa family has 600 loaded instances of incrementFam.rfa. All the brains of the operation are in this family. Each one of these families is simply a line that has 3 parameters that place it in 3 dimensional space. The 600 instances are linked together into 10 profiles of 60 families each. Each group of 60 is incremented 0-9 for parameter incrementZ, which places the family vertically. Within each group of 60, each family is numbered 0-59 to describe a profile. The 0-30 and 30-0 are connected by a spline through points. The profiles are then lofted together to either make 2 surface or one continuous solid, depending on what you want to do or how whacked out the shapes you make are.
By messing with the formulas in incrementFam.rfa, then reloading into supershapesBuildz you can produce a pretty considerable range or shapes. Many fail due to self intersecting forms, which Revit does not like (having 2 things occupying the same time and space is not very buildable) so you may have lots of blown up forms. But don’t worry about that, as you can simply re-loft the profiles later or undo the load operation and try again with different numbers.
Download the base family from here.
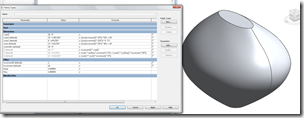
For those who have been wondering, this turns out to be the mathematical definition of the Venus of Willendorf








Comments
Post a Comment